Le puzzle de Sam Loyd , constitué de cinq pièces est présenté ci-dessous sous la forme d’un quadrilatère.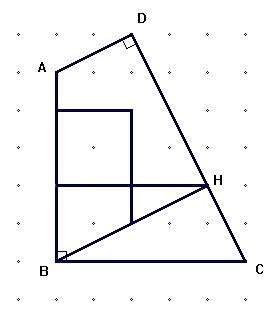

 

 

 

Ce quadrilatère a quelques particularités qui rendent intéressante son étude :

- il possède deux côtés consécutifs égaux

- deux de ses angles opposés sont droits

- les deux côtés qui ne sont pas égaux sont dans le rapport 3.

 

 

* Différentes approches sont possibles :

-  tracé à la règle et au compas

- construction sur quadrillage

- distribution des pièces du puzzle puis reconstruction du quadrilatère de base

 

 

* Différentes exploitations, et à plusieurs niveaux sont possibles : on peut se contenter des figures à reconstituer, rester sous la forme du jeu du puzzle

- fabriquer un carré, un rectangle, une croix grecque, un rectangle et un T ,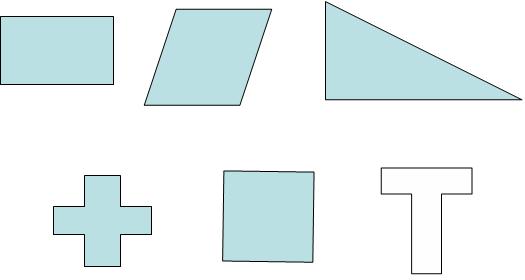

 

 

- ou bien aller plus loin dans les justifications et utilisations de transformations identifiées pour passer d’une figure à l’autre.

 

( voir document joint )

 

* C’est aussi l’occasion de faire réaliser aux élèves un pavage du plan, ou bien être un point de départ vers d’autres types de pavage...

( voir document joint )

 

 

* L’intérêt de la construction sur quadrillage est la possibilité offerte à la justification :

 

-- dans une première phase d’analyse , pour :

- angles droits en D et en H par étude d’angles complémentaires

- CD = 3 AD

 

-- dans un deuxième temps pour une éventuelle fabrication sur papier cartonné quadrillé

( à noter que le découpage de plaques de polypropylène se prête très bien à ce puzzle )

 

 

-- et enfin pour caractériser les transformations utilisées : 

 

- calcul des angles de rotation

- détermination des vecteurs de translation...